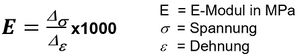Zugversuch: Unterschied zwischen den Versionen
Horsch (Diskussion | Beiträge) (→Normung des Zugversuches) |
Horsch (Diskussion | Beiträge) (→Ermittelte Kennwerte aus dem Zugversuch) |
||
| Zeile 69: | Zeile 69: | ||
|'''MPa''' | |'''MPa''' | ||
|meist ReH , bei Werkstoffen mit ausgeprägter oberer Streckgrenze | |meist ReH , bei Werkstoffen mit ausgeprägter oberer Streckgrenze | ||
| − | + | *'''ReH''' obere Streckgrenze | |
| − | + | *'''ReL''' untere Streckgrenze | |
| − | |||
|- | |- | ||
|'''Dehngrenzen''' | |'''Dehngrenzen''' | ||
|'''Rp''' | |'''Rp''' | ||
|'''Mpa''' | |'''Mpa''' | ||
| − | |''' | + | |'''Rp 0,2''' bei Werkstoffen ohne ausgeprägte Streckgrenze wird die Rp0,2 ermittelt, sie wird auch als technische Streckgrenze bezeichnet.<br />'''Rp 0,01''' technische Elastizitätsgrenze, gerade eben ermittelbare plastische Verformung, kennzeichnet den Übergang von der Mikroplastizität zum makroskopischen Fließen des Werkstoffes. |
| − | ''' | ||
|- | |- | ||
|'''Dehnung''' | |'''Dehnung''' | ||
| Zeile 92: | Zeile 90: | ||
|'''E''' | |'''E''' | ||
|'''Mpa''' | |'''Mpa''' | ||
| − | |Proportionalitätsfaktor '''''E''''', er ist ein Maß für den Wiederstand, den ein Werkstoff seiner elastischen Verformung entgegensetzt | + | |Proportionalitätsfaktor '''''E''''', er ist ein Maß für den Wiederstand, den ein Werkstoff seiner elastischen Verformung entgegensetzt.<br />Der Elastizitätsmodul (auch Zugmodul, Elastizitätskoeffizient, Dehnungsmodul, E-Modul oder Youngscher Modul) ist ein Materialkennwert, der den Zusammenhang zwischen Spannung und Dehnung bei der Verformung eines festen Körpers bei linear-elastischem Verhalten beschreibt. |
| − | Der Elastizitätsmodul (auch Zugmodul, Elastizitätskoeffizient, Dehnungsmodul, E-Modul oder Youngscher Modul) ist ein Materialkennwert, der den Zusammenhang zwischen Spannung und Dehnung bei der Verformung eines festen Körpers bei linear-elastischem Verhalten beschreibt. | ||
|- | |- | ||
|'''Querkontraktionszahl'''<ref>https://de.wikipedia.org/wiki/Poissonzahl?oldformat=true, 05.04.2017</ref> | |'''Querkontraktionszahl'''<ref>https://de.wikipedia.org/wiki/Poissonzahl?oldformat=true, 05.04.2017</ref> | ||
Version vom 1. Juli 2017, 07:53 Uhr
Ich biete zu diesem Thema das Seminar Intensivseminar für Auszubildende und Labormitarbeiter an.
Schauen Sie auf meiner Homepage vorbei und sichern Sie sich Ihren Platz!
Verlinkte Seiten
Inhaltsverzeichnis
Einleitung
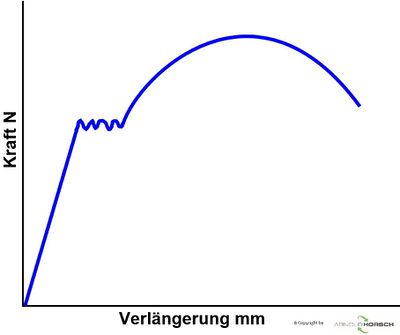
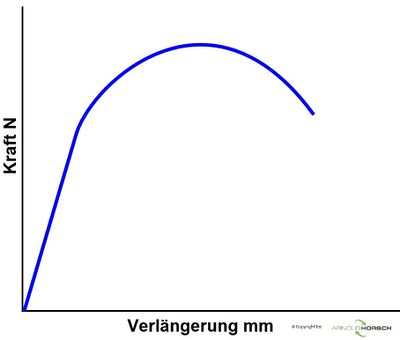
Der Zugversuch ist eines der wichtigsten mechanischen Prüfverfahren. Aus dem Zugversuch werden Kennwerte unter einachsiger Belastung bei konstanter Temperatur (meist Raumtemperatur) bestimmt. Dazu wird ein glatter, d.h. ungekerbter Prüfstab in eine Zugprüfmaschine eingespannt und in Richtung der Stabachse mit konstanter Verformungsgeschwindigkeit bis zum Zerreißen gedehnt. Die Zugprüfmaschine erfasst den Zusammenhang zwischen Zugkraft F und Verlängerung ΔL der Probe als Kraft‐Verlängerungs‐Diagramm, mitunter auch als Maschinendiagramm bezeichnet. Kraft und Verlängerung sind aber nicht Werkstoffspezifisch, sondern werden von der Probengeometrie (Anfangsmesslänge, Anfangsquerschnitt) bestimmt. Indem die Zugkraft auf den Probenquerschnitt und die Verlängerung auf die Probenlänge bezogen werden, erhält man das Spannungs‐Dehnungs-Diagramm für den entsprechenden Werkstoff. Bei diesen Diagrammen unterscheidet man das technische Spannungs‐Dehnungs‐Diagramm, das wahre Spannungs‐Dehnungs‐Diagramm und die Fließkurve[1] [2].
Historie
Durchführung des Zugversuches
Die Probe wird mit einer Normalspannung (senkrecht zur Querschnittfläche wirkenden Kraft) belastet. Das Prüfprinzip ist relativ simpel, die Probe wird[2]-
- angefertigt
- vermessen
- eingespannt
- gezogen
Der Zugversuch wird in der Regel an einer genormten Probe des zu prüfenden Werkstoffes durchgeführt. Hierzu wird die Probe in eine hydraulische oder mechanisch arbeitende Zugprüfmaschine eingespannt und mit zunehmender Zugkraft so lange verformt, bis der Bruch der Probe eintritt. Die erforderliche Zugkraft F wird in abhängigkeit der Probenverlängerung ΔL kontinuierlich registriert und mann erhält das Kraft-Verlängerungs-Diagramm[2][3].
| Werkstoff mit ausgeprägter Streckgrenze | Werkstoff ohne ausgeprägte Streckgrenze |
|
|
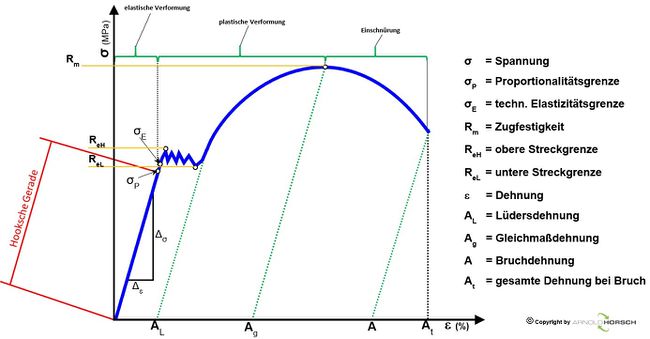
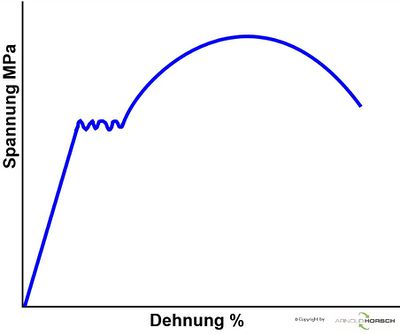
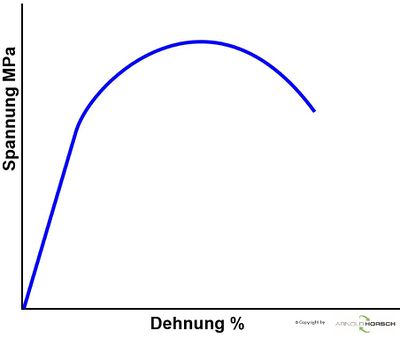
Sowohl die Zugkraft als auch die Probenverlängerung ist von der Probenabmessung abhängig. Das Kraft-Verlängerungs-Diagramm liefert daher keine Werkstoffkennwerte mit dessen Hilfe ein quantitativer Werkstoffvergleich möglich wäre. Um von der Probengeometrie unabhängige Kenngrößen zu ermitteln, bezieht man die Zugkraft F daher auf die Probenquerschnittsfläche So der Probe vor der Prüfung und spricht von der (mechanischen) Spannung σ und man erhält das Spannungs-Dehnungs-Diagramm[3].
| Werkstoff mit ausgeprägter Streckgrenze | Werkstoff ohne ausgeprägte Streckgrenze | Aus dem Spannungs-Dehnungs-Diagramm können jetzt die entsprechenden Werkstoffkennwerte abgelesen werden[2]. |
|
|
 |
Ermittelte Kennwerte aus dem Zugversuch
Folgende Kennwerte werden im Zugversuch ermittelt[2] -
| Was | Kurzzeichen | Dimension | Beschreibung |
| Zugfestigkeit | Rm | MPa | Als Zugfestigkeit Rm bezeichnet man das Spannungsmaximum im Spannungs-Dehnungs-Diagramm, d.h. die Höchszugkraft bezogen auf den Anfangsquerschnitt So. Nach überschreiten der Zugfestigkeit erfolgt der Bruch der Probe. Abhängig von der Werkstoffart oder Werkstoffzustand unterscheided man verschiedene Bruchformen. |
| Streckgrenze | Re | MPa | meist ReH , bei Werkstoffen mit ausgeprägter oberer Streckgrenze
|
| Dehngrenzen | Rp | Mpa | Rp 0,2 bei Werkstoffen ohne ausgeprägte Streckgrenze wird die Rp0,2 ermittelt, sie wird auch als technische Streckgrenze bezeichnet. Rp 0,01 technische Elastizitätsgrenze, gerade eben ermittelbare plastische Verformung, kennzeichnet den Übergang von der Mikroplastizität zum makroskopischen Fließen des Werkstoffes. |
| Dehnung | A | % | Unter der Bruchdehnung A versteht man die bleibende Dehnung der Zugprobe nach dem Bruch. |
| Einschnürung | Z | % | Die Brucheinschnürung (Verformungszähigkeit) Z ist die größte bleibende Querschnittsänderung nach dem Bruch der Zugprobe. |
| Elastizitätzmodul | E | Mpa | Proportionalitätsfaktor E, er ist ein Maß für den Wiederstand, den ein Werkstoff seiner elastischen Verformung entgegensetzt. Der Elastizitätsmodul (auch Zugmodul, Elastizitätskoeffizient, Dehnungsmodul, E-Modul oder Youngscher Modul) ist ein Materialkennwert, der den Zusammenhang zwischen Spannung und Dehnung bei der Verformung eines festen Körpers bei linear-elastischem Verhalten beschreibt. |
| Querkontraktionszahl[4] | μ | Die Poissonzahl ν (auch Querkontraktionszahl, Querdehnungszahl oder Querdehnzahl genannt; auch mit μ bezeichnet) ist eine Größe in der Mechanik bzw. Festigkeitslehre. Sie dient der Berechnung der Querkontraktion und ist nach Siméon Denis Poisson benannt. Sie gehört zu den elastischen Konstanten eines Materials. | |
| Proportionalitätsgrenze | σP | MPa | Punkt im Spannungs-Dehnungs-Diagramm, der das Ende der Hoock'schen Geraden definiert. Ab hier sind Kraft und Weg nicht mehr proportional es findet eine bleibende Verformung statt. |
| Elastizitätsgrenze | σE | MPa | Als Elastizitätsgrenze eines Werkstoffes bezeichnet man die Größe der mechanischen Spannung, unterhalb der das Material elastisch ist, d. h., es nimmt wieder die ursprüngliche Form ein, wenn die Belastung entfernt wird (nicht-bleibende/reversible Verformung). Beim Überschreiten der Elastizitätsgrenze tritt eine irreversible Dehnung oder Stauchung bzw. eine plastische Verformung auf. Die Elastizitätsgrenzwerte werden neben anderen Materialkennwerten für die Berechnung und Bestimmung der Festigkeit und Stabilität mechanischer Konstruktionen verwendet. Im Spannungs-Dehnungs-Diagramm ist die Elastizitätsgrenze der Punkt, in dem die Spannungskurve vom linearen Verlauf abweicht. Dieser Punkt ist nicht eindeutig definiert, sondern von der Messmethode abhängig. |
Auswertung
Kurzzeichen für den Zugversuch
| Was | Kurzzeichen |
| Probendurchmesser | do |
| Durchmesser nach Bruch | du |
| Anfangsquerschnitt | So |
| Querschnitt nach Bruch | Su |
| Anfangsmesslänge | Lo |
| Messlänge nach Bruch | Lu |
| Maximalkraft nach Bruch | F |
| Paralle Länge | Lc |
Berechnung der Kennwerte aus Zugversuch
| Was | Erklärung | Formel | Dimension |
| Zugfestigkeit | Die von Probengeometrie unabhängige Zugfestigkeit Rm (Spannung σ MPa), wird als das Verhältnis der Bruchkraft Fmax / Anfangsquerschnitt So ermittelt |
|
MPa |
| Streckgrenze | Die von Probengeometrie unabhängige Streckgrenze Re (Spannung σ MPa), wird als das Verhältnis der Kraft F am Punkt ReH - ReL/ Anfangsquerschnitt So ermittelt |
|
MPa |
| Dehngrenze | Die von Probengeometrie unabhängige Dehngrenze Rp (Spannung σ MPa), wird als das Verhältnis der Kraft F am Punkt Rp (Rp0,2 - Rp0,01) / Anfangsquerschnitt So ermittelt |
|
MPa |
| Dehnung | Die von Probengeometrie unabhängige DehnungA (Dehnung ε %), wird als das Verhältnis der Probenverlängerung ΔL / AnfangsmesslängeLo ermittelt |
|
% |
| Einschnürung | Die von Probengeometrie unabhängige Brucheinschnürung Z (Einschürung %), wird als das Verhältnis der relativen Querschnittsänderung ΔS / Anfangsquerschnitt So ermittelt |
|
% |
| E Modul | Der von Probengeometrie unabhängige Elastizitätsmodul E (E-Modul MPa), wird als das Verhältnis von Spannung Δσ / Dehnung Δε ermittelt |
|
MPA |
| ' | |||
| ' |
Normung des Zugversuches
Folgende Normen regeln Grundsätzlich den Zugversuch an metallischen Werkstoffen, verschieden Produktnormen können andere als in diesen Normen vorgegebene Versuchsparameter fordern.
| Norm | Bezeichnung | Teile |
|---|---|---|
| DIN 50125 | Prüfung metallischer Werkstoffe – Zugproben | |
| DIN EN ISO 6892 | Metallische Werkstoffe – Zugversuch | Teil 1 - Prüfverfahren bei Raumtemperatur Teil 2 - Prüfverfahren bei erhöhter Temperatur Teil 3 - Prüfverfahren bei tiefen Temperaturen Teil 4 - Prüfverfahren in flüssigem Helium (nur ISO Norm) |
Probenformen
Grundsätzlich sind die Probenformen in der Internationalen Norm ISO 6592 nicht genormt. In Deutschland existiert jedoch die DIN 50125 Prüfung metallischer Werkstoffe – Zugproben, es wird empfohlen sich an die in dieser Norm angegebenen Probenformen soweit als möglich zu halten. Außerhalb der in der DIN 50125 vorgegebenen Probenformen, existieren noch eine Vielzahl von Produktnormen in denen spezielle Probenformen vorgegeben werden[2].
- DIN 50125 Prüfung metallischer Werkstoffe – Zugproben
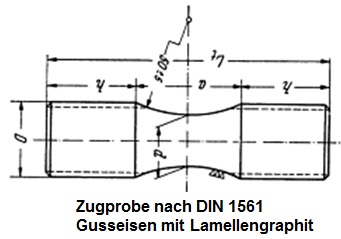
- DIN EN 1561 Zugproben aus Gusseisen mit Lamellengraphit
- DIN EN 1562 Zugproben aus Temperguss
- DIN EN 1563 Zugproben aus Gusseisen mit Kugelgraphit
- DIN EN 1564 Zugproben aus bainitischem Gusseisen
- DIN 50148 Zugproben für Druckguss aus Nichteisenmetallen
- DIN EN 895 Zugproben zur Prüfung von Schweißverbindungen metallischer Werkstoffe
- DIN 8525-1 Zugproben zur Prüfung von Hartlötverbindungen
| Norm | Beschreibung Probenforn |
| DIN 50125 Prüfung metallischer Werkstoffe – Zugproben |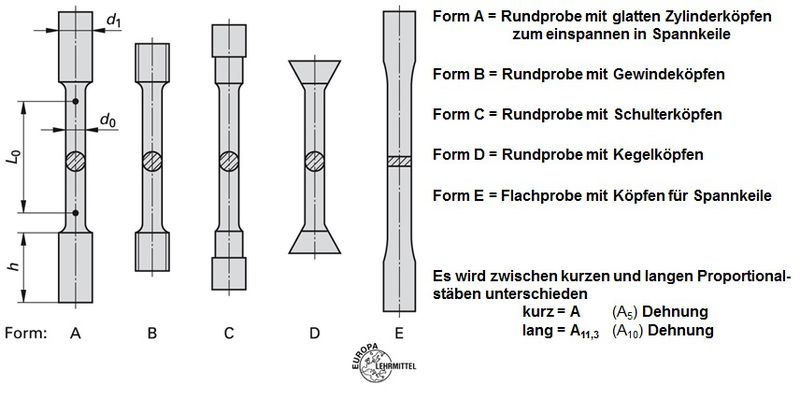 
|
| DIN 1561 Zugproben aus Gusseisen mit Lamellengraphit |  |
Einzelnachweise
- ↑ 1,0 1,1 Professur für Biomaterialien, Praktikum Werkstoffwissenschaft, Zugversuch, TU Dresden
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 2,6 Arnold Horsch, Vorlesung Grundlagen der Werkstoffprüfung 1+2, als Lehrbeauftrager an der Hochschule Pforzheim, 17.03.2017
- ↑ 3,0 3,1 3,2 Arnold Horsch, Vortrag, Die Werkstoffprüfverfahren, Intensivseminar für Auszubildende und Labormitarbeiter, Arnold Horsch e.K., Remscheid
- ↑ https://de.wikipedia.org/wiki/Poissonzahl?oldformat=true, 05.04.2017
